Arash Abadpour, “Fuzzy Clustering for Responsive Data”, also filed as a provisional patent. (pdf) (printed copy) [Grace]
The unsupervised clustering of a weighted group of data items, into sets which comply with a notion of homogeneity specific to a particular problem class, is a classical pattern classification problem. Among the different approaches to this problem, fuzzy and possibilistic clustering, and their different variations and combinations, have been studied in the last decades. That study, however, has often been focused on a particular data item or cluster model and has been generally geared towards identifying a particular model of homogeneity. Also, many available models are in essence engineered based on the intuition of the researchers and convoluted and complicated control parameters, regularization terms, and concepts are often incorporated into the mathematical models in order to yield acceptable results. In this paper, we advocate for a derivation-based approach, which utilizes Bayesian inference in order to assess the loss in a generic clustering problem, independent of the particularities of data and cluster models and the notion of homogeneity applicable to any particular problem class. Subsequently, we utilize the organic framework developed in this work in order to address data items which actively respond to the clustering effort. This is distinctly different from the available literature, in which data items are passively subjected to the clustering process. The utilization of an inference-based loss model, which avoids exogenous provisions based on intuition and researcher heuristics, as well as independence from a particular problem class and the introduction of the concept of data responsiveness, to our understanding, are novel to this paper.
Arash Abadpour, “On Addressing Cluster Count Ambiguity using Fuzzy Cluster Relevance Factors”. (pdf) (printed copy)[Selma]
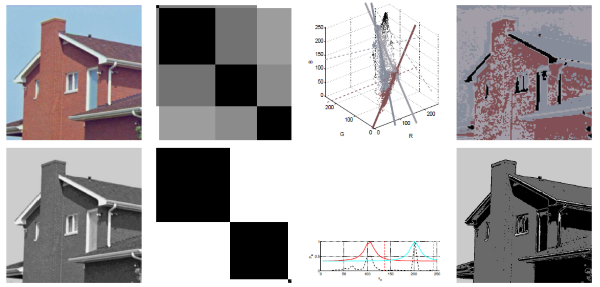
Unsupervised clustering of a set of data items of an arbitrary model into clusters which comply with a particular model of homogeneity is a useful tool in many applications within many fields, including the general field of computer sciences. This problem, however, is in essence ill-posed, due to the fact that it concerns the determination of cluster representations as well as data item-to-cluster correspondences, two entities which are heavily entangled. The research community is well aware of this ambiguity and has responded with several important contributions, such as the fuzzy membership regime and varied approaches to robustification, among others. Some of these works, however, utilize models and parameters which are in essence based on the intuition of the researchers and result in the presence of regularization coefficients and variables and configuration parameters which are defined metaphorically. In this work, we utilize a derivation-based approach and perform Bayesian loss modeling in order to derive the objective function for a fuzzy clustering algorithm which utilizes fuzzy data. The third component of the fuzziness regime explored in this paper, which to the best of our knowledge is novel to this work, is the fuzzification of the clusters. We demonstrate that fuzzy clustering of fuzzy data into fuzzy clusters is a proper continuation of the movement within the data clustering community that resulted in important achievements in terms of the performance of clustering algorithms.
Arash Abadpour, “Towards Generalized VAT-style Class-independent Unsupervised Fuzzy Clustering for Big Data”. (pdf) (printed copy) [Annina]
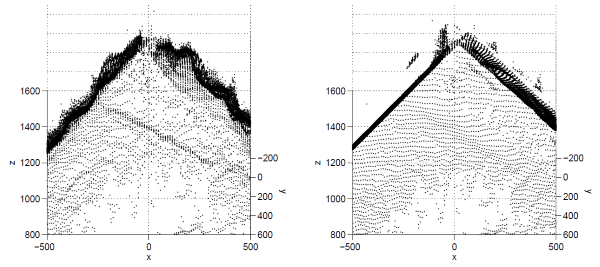
It is a prerequisite to many applications in different fields to separate a set of data items into homogenous clusters. In this context, a data item may be a member of $\R^k$ or a complex mathematical entity encompassing several properties. Homogeneity, too, is a general concept which is defined differently in different contexts. In effect, the ability to work with abstract models for data items and clusters has important economical benefits, in terms of not only the reusability of the algorithms, but also the reuse of actual computer code. Visual Assessment of Cluster Tendency (VAT) is a discovery mechanism which has been shown to work desirably within the context of prototype-based clustering. However, VAT has been shown to suffer from high costs of operation, especially in the context of Big Data. While the research community has invested heavily on proposing alternatives to VAT, a generic cost-effective unsupervised cluster discovery algorithm is not within reach. In this work, we demonstrate that the VAT comparison and reordering mechanism can be applied at the level of clusters, instead of its classical application at the level of data items. We exhibit that this innovation results in effective reduction of the computational complexity of the resulting algorithm from $O(N^2)$ to $O(N)$. Moreover, we demonstrate that this technique allows for a generic formulation of the unsupervised clustering problem. This paper includes the mathematical derivation of this idea accompanied by experimental results. We provide some of the deficiencies of the present work at the end of the paper and recommend potential ideas for the continuation of this work.
Arash Abadpour, “Towards Unsupervised Fuzzy Discovery of an Undetermined Number of Clusters for a Generic Non-Relational Notion of Homogeneity”. (pdf) (printed copy) [Donna]
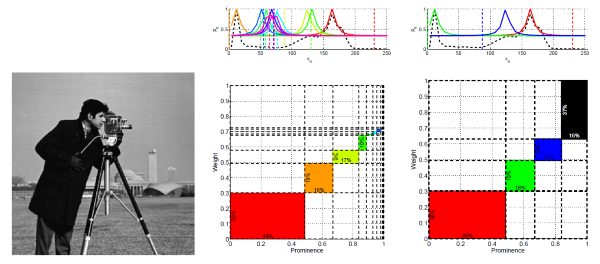
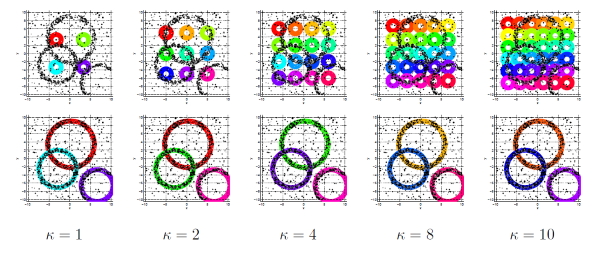
Fuzzy clustering is a mature field of study which involves the unsupervised grouping of a number of observations into homogenous clusters. This prerequisite for a diverse set of problems in many fields of computer and other sciences has been traditionally concerned with notions of homogeneity which are relational. Additionally, fuzzy clustering took off based on the assumption that one is going to know, with a great deal of certainty, how many clusters are present in an input set of data items, what is denoted as the C number in this work. As clustering algorithms made significant progress towards separating a known number of clusters from the data, it was observed that this assumption is in fact at the same time both non-trivial and critically important. Subsequent works, including the important category of VAT algorithms, attempted, with various degrees of success in many cases, to produce a usable estimate for the number of clusters prior to any clustering having happened. Nevertheless, the determination of the number of clusters appropriate for an arbitrary problem instance is a challenge to date, specifically when a non-relational and generic notion of homogeneity is applicable. In this paper, we argue that the number of clusters present in a set of data items, that corresponds to a physical phenomenon, is in fact not a deterministic number to be known. In other words, the problem is not to find “the C clusters” present in a given set of data items, but, instead, to discover clusters in the data and to allow the user to select how many of the discovered clusters are applicable to their case. In other words, C is not an entity to be sought for, but, we argue that, it is the mirage of certainty which has afflicted the fuzzy clustering literature. Thus, we eliminate $C$ from the model and utilize the results of multiple independent executions of a robustified single-cluster clustering model which we aggregate using a non-relational class-independent framework. This process results in many clusters, for each one of which associated prominence and weight indicators are calculated.
Arash Abadpour, “Fuzzy Clustering using Levenberg-Marquardt Optimization and Deterministic Annealing”. (pdf) (printed copy)[Ava]

In this paper, we address the generic problem of unsupervised data clustering within a fuzzy framework. We show that this problem can be formulated as a least mean square vector cost function and propose an iterative solution procedure which utilizes the Levenberg-Marquardt optimization technique. As such, we develop an algorithm which is capable of performing the stated task through utilizing abstract notions of data item, cluster, and data item-to-cluster distance. We demonstrate that the fuzzifier can be utilized as a temperature factor, in order to set up a Deterministic Annealing framework that provides assurance that the derived loss function converges to an acceptable minimum. This is important because the developed method includes an additional layer of numerical optimization on top of the structure commonly used in the literature. This paper includes the derivation of the cost function as well as the outline of the developed solution procedure. We carry sample problem instances from six problem classes and discuss different aspects of the developed method. Finally, we provide a potential next step for this work.
