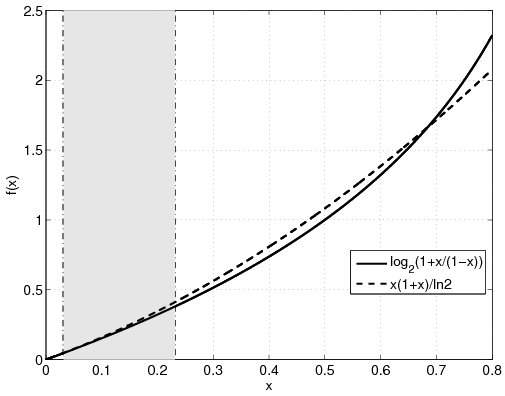
 | 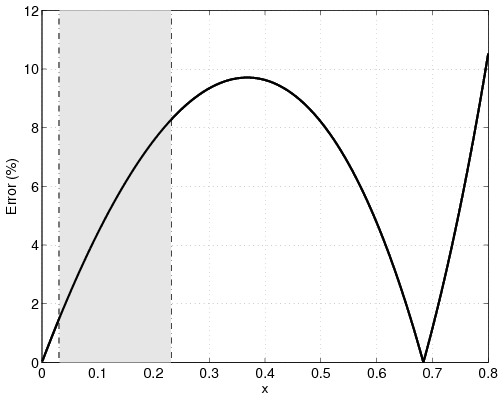 |
| (a) | (b) |
|
|
|
|
|
|
|
| (8) |
|
|
|
|
 |  |
| (a) | (b) |
|
|
| (15) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Station # | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| gi (×10-11) | 0.4 | 0.0051 | 0.0038 | 0.0019 | 0.0014 | 0.0008 | 0.00052 | ||
| pi | 5.77 | 5.90 | 7.85 | 16.02 | 21.28 | 37.19 | 57.24 | ||
| E | Ci | 2.147 | 0.014 | 0.014 | 0.014 | 0.014 | 0.014 | 0.014 | |
| CSCa | C | 2.233 | |||||||
| pia | 5.77 (0%) | 5.90 (0%) | 7.85 (0%) | 16.02 (0%) | 21.28 (0%) | 37.19 (0%) | 57.24 (0%) | ||
| A | Cia | 1.982 (8%) | 0.014 (0%) | 0.014 (0%) | 0.014 (0%) | 0.014 (0%) | 0.014 (0%) | 0.014 (0%) | |
| Ca | 2.068 (8%) | ||||||||
| A+E | Cia* | 2.147 (0%) | 0.014 (0%) | 0.014 (0%) | 0.014 (0%) | 0.014 (0%) | 0.014 (0%) | 0.014 (0%) | |
| Ca* | 2.233 (0%) | ||||||||
| pi | 1.40 | 111.86 | 148.95 | 199.53 | 199.53 | 166.60 | 57.24 | ||
| E | Ci | 0.300 | 0.300 | 0.300 | 0.190 | 0.141 | 0.065 | 0.014 | |
| NSCa | C | 1.310 | |||||||
| pia | 1.40 (0%) | 111.86 (0%) | 148.95 (0%) | 199.53 (0%) | 199.53 (0%) | 166.60 (0%) | 57.24 (0%) | ||
| A | Cia | 0.322 (7%) | 0.322 (7%) | 0.322 (7%) | 0.200 (5%) | 0.146 (4%) | 0.067 (2%) | 0.014 (0%) | |
| Ca | 1.393 (6%) | ||||||||
| A+E | Cia* | 0.300 (0%) | 0.300 (0%) | 0.300 (0%) | 0.190 (0%) | 0.141 (0%) | 0.065 (0%) | 0.014 (0%) | |
| Ca* | 1.310 (0%) | ||||||||
| pi | 1.33 | 106.43 | 141.72 | 199.53 | 199.53 | 199.53 | 164.49 | ||
| E | Ci | 0.284 | 0.284 | 0.284 | 0.190 | 0.141 | 0.079 | 0.042 | |
| N+SCa | C | 1.303 | |||||||
| pia | 1.33 (0%) | 106.43 (0%) | 141.72 (0%) | 199.53 (0%) | 199.53 (0%) | 199.53 (0%) | 164.49 (0%) | ||
| A | Cia | 0.304 (7%) | 0.304 (7%) | 0.304 (7%) | 0.200 (5%) | 0.146 (4%) | 0.081 (2%) | 0.042 (1%) | |
| Ca | 1.303 (0%) | ||||||||
| A+E | Cia* | 0.284 (0%) | 0.284 (0%) | 0.284 (0%) | 0.190 (0%) | 0.141 (0%) | 0.079 (0%) | 0.042 (0%) | |
| Ca* | 1.303 (0%) | ||||||||